斐波那契数列总结

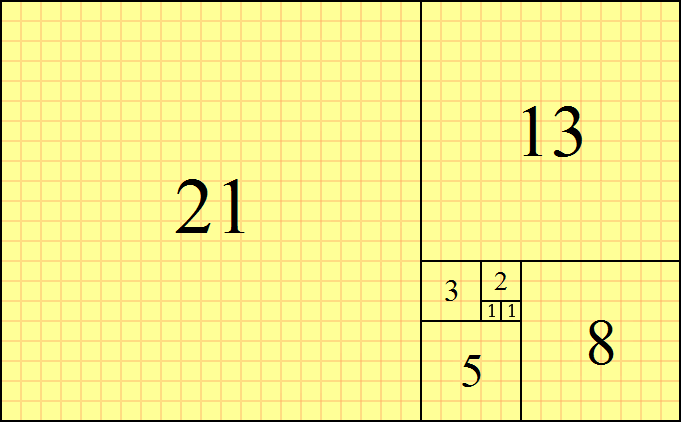
斐波那契数列是从0，1开始，后面每一项都是由前面两项相加得到。开头几项是0、1、1、2、3、5、8、13……。在OEIS中是A000045数列。需要注意的是斐波那契数列的第零项是0，第一项是1。本文将探讨总结斐波那契数列的相关问题。

递归定义如下：

$$ F_n = \begin{cases} 0, & n = 0 \\ 1, & n = 1 \\ F_{n-1} + F_{n-2} & n > 1 \end{cases} $$

小范围求$f(n)$#

$n \le 39$#

对应题目：牛客网 【编程题】斐波那契数列

在这个范围内的斐波那契数列可以很容易计算出来，速度也非常快(1秒以内)，根据定义可以写出下面的递归程序：

#include <bits/stdc++.h>
using namespace std;
int f(int n) {
    if (n < 2) return n;
    return f(n-1) + f(n-2);
}
int main() {
    cout << f(39) << '\n';
    cerr << "Time: " << (double)clock() / CLOCKS_PER_SEC << '\n';
    return 0;
}

运行结果：

63245986
Time: 0.184

注意：提交时需要改成类的版本。

$n \le 46$#

对应题目：计蒜客T1066 斐波那契数列

看似数据范围仅仅增大了7，但我们继续使用上面的程序计算$f(46)$时，会得到如下结果：

1836311903
Time: 4.946

时间已经超出了1秒的限制，考虑优化一下计算方法。实际上在递归调用的过程中，有很多值被重复计算了。我们可以记录下已经算过的值，当下次需要时直接读取，不再重复计算。

#include <bits/stdc++.h>
using namespace std;
int fib[47];
int f(int n) {
    if (n < 2) return n;
    else if (fib[n]) return fib[n]; // 已经算过
    else return fib[n] = f(n - 1) + f(n - 2);
}
int main() {
    int n = 46;
    // cin >> n;
    cout << f(n) << '\n';
    cerr << "Time: " << (double)clock() / CLOCKS_PER_SEC << '\n';
    return 0;
}

再次测试$f(46)$，发现这次计算的非常快！

1836311903
Time: 0.001

$n \le 100$#

对应题目：力扣 剑指 Offer 10- I. 斐波那契数列

注意到答案开始需要对$10^9+7$取模了，但我们仍然可以使用上面的写法（加个取模）即可通过此题。

点击展开代码 >folded

#include <bits/stdc++.h>
using namespace std;
const int M = 1e9 + 7;
int fib[101];
int f(int n) {
    if (n < 2) return n;
    else if (fib[n]) return fib[n]; // 已经算过
    else return fib[n] = (f(n - 1) + f(n - 2)) % M;
}
int main() {
    int n = 100;
    // cin >> n;
    cout << f(n) << '\n';
    cerr << "Time: " << (double)clock() / CLOCKS_PER_SEC << '\n';
    return 0;
}
// 运行结果：
// 687995182
// Time: 0.001

这次我们尝试换一种写法，不使用数组，利用两个变量递推得出结果。时间复杂度和上面的代码一样，但空间复杂度更加优秀。

#include <bits/stdc++.h>
using namespace std;
const int M = 1e9 + 7;
int main() {
    int n = 100, a = 0, b = 1;
    // cin >> n;
    while (n--) {
        a = (a + b) % M;
        swap(a, b);
    }
    cout << a << '\n';
    cerr << "Time: " << (double)clock() / CLOCKS_PER_SEC << '\n';
    return 0;
}
// 运行结果：
// 687995182
// Time: 0

一开始a代表$f(0)$，每循环一次，a表示的数就往后一位，所以循环n次后，a就表示$f(n)$。

$n \le 4786$#

对应题目：HHUOJ-1387 大斐波那契数
注：题目仅给出结果不超过1000位。

容易发现C++中的int甚至long long都无法保存这么大的数了，但好在评测系统是支持Python的，考虑到Python写法简单且自带大数，我们可以尝试使用Python来写这题。

前面提到，斐波那契数列后面每一项都是由前面两项相加得到。我们可以根据这条规则来写代码。

from itertools import count
f = [0, 1]
for i in count(2):
    f.append(f[-1] + f[-2])
    if len(str(f[i])) > 1000: break
for n in [*open(0)]:
    print(f[int(n)])

其中f[-1]表示取序列f中最后一个元素，count(2)产生一个从2开始的无限序列，[*open(0)]表示打开标准输入文件并按行分割成列表。

其他写法#

还有很多有趣的写法来求小范围的斐波那契数列，这里列举几种，就不详细展开了。

• Python 生成器

def fib(n):
    i, a, b = 0, 0, 1
    while i < n:
        yield a
        a, b = b, a + b
        i = i + 1
print(list(fib(10)))

大范围求$f(n)$#

前面提到的算法的时间复杂度是$O(n)$的，理论上来说可以在1秒以内求出$10^8$以内的值，所以这里的大范围肯定是要比$10^8$还大的。

$n \le 10^9$#

对应题目：POJ-3070 Fibonacci
注意此题的模数是10000。

题目中已经给出了关于Fibonacci数列的另一个很重要的公式：

$$ \begin{pmatrix} F_{n+1} & F_n \\ F_n & F_{n-1} \end{pmatrix}= \begin{pmatrix} 1 & 1\\ 1 & 0 \end{pmatrix} ^n $$

考虑到n比较大，可以使用矩阵快速幂求解。矩阵快速幂是快速幂算法的变形，仍然是利用如下原理：

$$ x^y = \begin{cases} x \cdot x^{y-1}, & y为奇数 \\ x^{y/2} \cdot x^{y/2}, & y为偶数 \end{cases} $$

通常我习惯把它写成while循环结合位运算的形式。时间复杂度为$O(\log(n))$

#include <cstring>
#include <iostream>
using namespace std;
const int M = 1e4;
typedef int mat[2][2];
#define FOR(i, n) for(int i = 0; i < n; i++)
void muleq(mat &a, mat &b) {
    mat c{};
    FOR(i, 2) FOR(j, 2) FOR(k, 2)
        c[i][j] = (c[i][j] + a[i][k] * b[k][j] % M) % M;
    memcpy(a, c, sizeof(a));
}
int main() {
    int n;
    while (cin >> n) {
        if (n == -1) break;
        mat a{{1, 1}, {1, 0}};
        mat ans{{1, 0}, {0, 1}};
        while (n) {
            if (n & 1) muleq(ans, a);
            muleq(a, a);
            n >>= 1;
        }
        cout << ans[1][0] << '\n';
    }
    return 0;
}

由于POJ的编译器比较老，采用了不那么直观的写法。muleq(a, b)的含义是a = a * b，其中a、b均为矩阵，*为矩阵乘法。

$n \le 10^{18}$#

对应题目：51Nod 1242 斐波那契数列的第N项
利用上面的做法同样可以通过此题，这里利用运算符重载给出更直观一点的代码。
注意：此题的模数为$10^9+9$。

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const ll M = 1e9 + 9;
using Mat = array<array<ll, 2>, 2>;
#define FOR(i, n) for(int i = 0; i < n; i++)
Mat operator*(const Mat &a, const Mat &b) {
    Mat c{};
    FOR(i, 2) FOR(j, 2) FOR(k, 2)
        c[i][j] = (c[i][j] + a[i][k] * b[k][j]) % M;
    return c;
}
Mat Pow(Mat x, ll y) {
    Mat ans{{{1, 0}, {0, 1}}};
    while (y) {
        if (y & 1) ans = ans * x;
        x = x * x;
        y >>= 1;
    }
    return ans;
}
int main() {
    ll n = 1e18;
    // cin >> n;
    cout << Pow(Mat{{{1, 1}, {1, 0}}}, n)[0][1] << '\n';
    cerr << "Time: " << (double)clock() / CLOCKS_PER_SEC << '\n';
    return 0;
}
// 运行结果：
// 209762233
// Time: 0.001

$n \le 10^{10^{6}}$#

类似题目：2019牛客多校5B generator 1
对于这个范围的数，其实上面的算法也是可以解决的，就是实现上需要一些技巧。由于给定的n是一个十进制的数，将他转换成二进制需要花费大量时间，因此我们可以直接使用十进制下的快速幂来计算。

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const ll M = 1e9 + 7;
using Mat = array<array<ll, 2>, 2>;
#define FOR(i, n) for(int i = 0; i < n; i++)
string n;
int len;
Mat operator*(const Mat &a, const Mat &b) {
    Mat c{};
    FOR(i, 2) FOR(j, 2) FOR(k, 2)
        c[i][j] = (c[i][j] + a[i][k] * b[k][j]) % M;
    return c;
}
Mat Pow(Mat x, int y) {
    Mat ans{{{1, 0}, {0, 1}}};
    FOR(t, y) ans = ans * x;
    return ans;
}
ll Pow(ll x, ll y) {
    ll ans = 1;
    while (y) {
        if (y & 1) ans = ans * x % M;
        x = x * x % M;
        y >>= 1;
    }
    return ans;
}
Mat Pow(Mat x) {
    Mat ans{{{1, 0}, {0, 1}}};
    FOR(i, len) {
        ans = ans*Pow(x, n[i]-'0');
        x = Pow(x, 10);
    }
    return ans;
}
int main() {
    n = "1" + string(1e6, '0');
    len = (int)n.length();
    reverse(n.begin(), n.end());
    Mat A = Pow(Mat{{{1, 1}, {1, 0}}});
    cout << A[1][0] << '\n';
    return 0;
}

其他写法#

• 不使用矩阵的矩阵快速幂。由于斐波那契数列的矩阵递推式非常小（$2\times 2$），我们可以利用函数参数在递归时巧妙的计算。（对应题目：51Nod 1242 斐波那契数列的第N项）

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const ll M = 1e9 + 9;
ll f(ll n, ll a = 1, ll b = 0, ll p = 0, ll q = 1) {
    if (!n) return b;
    if (n & 1) return f(n-1, (b*q+a*q+a*p)%M, (b*p+a*q)%M, p, q);
    return f(n/2, a, b, (p*p+q*q)%M, (q*q+2*q*p)%M);
}
int main() {
    ll n = 1e18;
    // cin >> n;
    cout << f(n) << '\n';
    cerr << "Time: " << (double)clock() / CLOCKS_PER_SEC << '\n';
    return 0;
}
// 运行结果：
// 209762233
// Time: 0.002

• 利用循环节计算。当模数给定且n的范围远大于模数时，可以采用找循环节的做法，相比于十进制快速幂会好写很多，但有时循环节是不固定的。

如果不知道或者忘记了如何求斐波那契数列在给定模数下的循环节，可以写一个暴力程序求出。参考下面的代码：

点击展开代码 >folded

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
ll fib(ll m) {
    ll a = 1, b = 1, c = 1;
    while (!(a == 0 && b == 1)) {
        c++;
        a = (a + b) % m;
        swap(a, b);
    }
    return c;
}
int main() {
    cout << (int)(1e4) << ' ' << fib(1e4) << '\n';
    cout << (int)(1e9+7) << ' ' << fib(1e9+7) << '\n';
    cout << (int)(1e9+9) << ' ' << fib(1e9+9) << '\n';
    cerr << "Time: " << (double)clock() / CLOCKS_PER_SEC << '\n';
    return 0;
}
// 运行结果：
// 10000 15000
// 1000000007 2000000016
// 1000000009 333333336
// Time: 7.443

斐波那契相关问题#

对于其他和斐波那契数列相关的问题，如广义斐波那契数列、斐波那契数列前缀和等，这里归类为斐波那契相关问题。通常需要用到一些斐波那契数列的性质，参考文章：斐波那契数_孙智宏。

广义斐波那契数列#

对应题目：51Nod-1126 求递推序列的第N项
注意：此题下标从1开始。
广义斐波那契数列是斐波那契数列的推广，定义如下：

$$ F_n = \begin{cases} A, & n = 0 \\ B, & n = 1 \\ C\cdot F_{n-1} + D \cdot F_{n-2}, & n > 1 \end{cases} $$

当A=0，B=C=D=1是变成普通的斐波那契数列，A=2，B=C=D=1时，变成卢卡斯序列。

广义斐波那契数列的处理方式基本一样。我们可以推一下这个序列的矩阵递推式：

$$ \begin{aligned} \begin{pmatrix} f_{n+1} \\ f_n \end{pmatrix} & = \begin{pmatrix} C & D\\ 1 & 0 \end{pmatrix} \begin{pmatrix} f_n \\ f_{n-1} \end{pmatrix}\\ & = \begin{pmatrix} C & D\\ 1 & 0 \end{pmatrix}^{n} \begin{pmatrix} B \\ A \end{pmatrix} \end{aligned} $$

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const ll M = 7;
using Mat = array<array<ll, 2>, 2>;
#define FOR(i, n) for(int i = 0; i < n; i++)
Mat operator*(const Mat &a, const Mat &b) {
    Mat c{};
    FOR(i, 2) FOR(j, 2) FOR(k, 2)
        c[i][j] = (c[i][j] + a[i][k] * b[k][j]) % M;
    return c;
}
int main() {
    int a, b, n;
    cin >> a >> b >> n;
    Mat m{{{a, b}, {1, 0}}};
    Mat ans{{{1, 0}, {0, 1}}};
    for (n--; n; n >>= 1) {
        if (n & 1) ans = ans * m;
        m = m * m;
    }
    cout << ((ans[1][0] + ans[1][1]) % M + M) % M << '\n';
    return 0;
}

求区间和#

对应题目：HITOJ-2060 Fibonacci Problem Again。
注意：此题斐波那契数列前两项为1，模数为$10^9$。

考虑一般的斐波那契数列区间和，可以直接转化成斐波那契数列求解：$S(n)=f(n+2)-1$，其中$S(n)=\sum\limits_{i=0}^n f(i)$。

直接套用一个上面的代码，复杂度$O(log(n))$

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const ll M = 1e9;
ll f(ll n, ll a = 1, ll b = 0, ll p = 0, ll q = 1) {
    if (!n) return b;
    if (n & 1) return f(n-1, (b*q+a*q+a*p)%M, (b*p+a*q)%M, p, q);
    return f(n/2, a, b, (p*p+q*q)%M, (q*q+2*q*p)%M);
}
int main() {
    ll a, b;
    while (cin >> a >> b) {
        if (a == 0 && b == 0) break;
        cout << (f(b+3)-f(a+2)+M)%M << '\n';
    }
    return 0;
}

循环节加速#

对应题目：Fibonacci Again

实际上广义斐波那契数列也是有循环节的。利用之前提到的方法，可以直接算出这个序列的循环节为8。而该序列的前8项为[7, 11, 18, 29, 47, 76, 123, 199]，其中能被3整除的有[2, 6] 项，即n % 4 == 2是为yes。

#include <bits/stdc++.h>
using namespace std;
int main() {
    int n;
    while (cin >> n) {
        cout << ((n % 4 == 2) ? "yes" : "no") << '\n';
    }
    return 0;
}

小范围求循环节#

对应题目：HDU3977 Evil teacher

对于一个给定的模数，如何求出循环节呢？利用枚举的方法显然太慢了，我们可以利用这篇论文：The Period of the Fibonacci Sequence Modulo j.pdf中提到的一些性质来加速求解。

(定理3) 设$j$是一个正数，且$j=\prod\limits_{i=1}^s p_i^{k_i}$，其中$p_i$是素数，设$m_i$表示$F_n(\mod p_i^{k_i})$的循环节，$m$表示$F_n(\mod j)$的循环节，则有$m=lcm(m_1, m_2, …, m_s)$。

利用这条性质，我们可以先把模数P质因数分解，转换为求模数为$p^k$的情况。

再根据这条推论：

设$G( p )$表示$F_n(\mod p)$的循环节，其中$p$为质数，则有$G(p^k)=G( p )\cdot p^{k-1}$。

（详细证明可以参考这篇博客）

此外还有一个小性质：$G( p ) \le 6p$（证明参考这里）可以帮助我们估算复杂度。

注意到P的最大素因子不超过$10^6$，且只有20组，估算一下最坏情况下的复杂度完全可以通过此题。

点击展开代码 >folded

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e6+5;
inline ll lcm(ll a, ll b) { return a / __gcd(a, b) * b; }
ll fib_perd(ll m) { // 求Fn mod m 循环节
    ll a = 1, b = 1, c = 1;
    while (!(a == 0 && b == 1)) {
        c++;
        a = (a + b) % m;
        swap(a, b);
    }
    return c;
}
vector<bool> is_prime;
vector<ll> prime;
void get_prime() { // 素数筛法
    is_prime.resize(N, true);
    is_prime[0] = is_prime[1] = false;
    for (ll i = 2; i < N; i++) {
        if (!is_prime[i]) continue;
        prime.push_back(i);
        for (ll j = i * i; j < N; j += i) is_prime[j] = false;
    }
}
int main() {
    get_prime();
    int t; cin >> t;
    for (int i = 1; i <= t; i++) {
        ll n; cin >> n;
        ll ans = 1;
        for (auto p : prime) { // 质因数分解
            if (n % p) continue;
            ll pk = 1; // 保存p^k
            while (n % p == 0) pk *= p, n /= p;
            ans = lcm(ans, pk / p * fib_perd(p));
        }
        cout << "Case #" << i << ": " << ans << '\n';
    }    
    return 0;
}

通项公式#

上面已经得到了斐波那契数列公式的矩阵形式，要得到通项公式，还需要进一步变换。这里采用线性代数的方法。

$$ \begin{aligned} \begin{pmatrix} F_{n+1} \\ F_n \end{pmatrix} & = \begin{pmatrix} 1 & 1\\ 1 & 0 \end{pmatrix}^n \begin{pmatrix} 1 \\ 0 \end{pmatrix} \end{aligned} $$

利用对角化计算方阵的幂。

设矩阵$A=\begin{pmatrix} 1 & 1\\ 1 & 0 \end{pmatrix}$，其特征方程为：$|\lambda E-A|$，其中$E$为单位矩阵。

计算得：

$$ \begin{aligned} |\lambda E-A| & = \left| \begin{matrix} \lambda-1 & -1\\ -1 & \lambda \end{matrix} \right| \\ & = \lambda^2-\lambda-1 \end{aligned} $$

解得$\lambda_1=\frac{1-\sqrt{5}}{2}$，$\lambda_2=\frac{1+\sqrt{5}}{2}$。

代入特征值$\lambda_1$，解齐次线性方程组$(\lambda E - A)X=0$：

$$ \lambda E - A = \begin{pmatrix} -\lambda_2 & -1 \\ -1 & \lambda_1 \end{pmatrix} $$

将矩阵第一行乘以$\lambda_1$加到第二行，矩阵变换为：

$$ \begin{pmatrix} -\lambda_2 & -1 \\ 0 & 0 \end{pmatrix} $$

即$x_2=-\lambda_2 x_1$，取$x_1=1$，则其基础解系为$X_1=\begin{pmatrix}1 \\ -\lambda_2\end{pmatrix}$。

取特征向量为$\xi_1=\begin{pmatrix}1 \\ -\lambda_2\end{pmatrix}$，对于$\lambda_2$同理可得$\xi_2=\begin{pmatrix}1 \\ -\lambda_1\end{pmatrix}$。

令

$$ \begin{aligned} P & = (\xi_1, \xi_2)\\ & = \begin{pmatrix}1 & 1\\ -\lambda_2 & -\lambda_1\end{pmatrix}\\ & = \begin{pmatrix}1 & 1\\ \lambda_2 & \lambda_1\end{pmatrix} \end{aligned} $$

利用增广矩阵求逆。

$$ \begin{aligned} (P|E) & = \begin{pmatrix} 1 & 1 & 1 & 0\\ \lambda_2 & \lambda_1 & 0 & 1 \end{pmatrix} \\ & = \begin{pmatrix} 1 & 1 & 1 & 0\\ 0 & -\sqrt{5} & -\lambda_2 & 1 \end{pmatrix} \\ & = \begin{pmatrix} 1 & 0 & \frac{\sqrt{5}-1}{2\sqrt{5}} & \frac{1}{\sqrt{5}}\\ 0 & -\sqrt{5} & -\lambda_2 & 1 \end{pmatrix} \\ & = \begin{pmatrix} 1 & 0 & \frac{\sqrt{5}-1}{2\sqrt{5}} & \frac{1}{\sqrt{5}}\\ 0 & 1 & \frac{1+\sqrt{5}}{2\sqrt{5}} & -\frac{1}{\sqrt{5}} \end{pmatrix} \\ \end{aligned} $$

依次进行的变换为：

• 第一行乘以$-\lambda_2$加到第二行
• 第二行乘以$\frac{1}{\sqrt{5}}$加到第一行
• 第三行乘以$-\frac{1}{\sqrt{5}}$

注：Wolfram验算

可得$P^{-1}=\begin{pmatrix} \frac{\sqrt{5}-1}{2\sqrt{5}} & \frac{1}{\sqrt{5}}\\ \frac{1+\sqrt{5}}{2\sqrt{5}} & -\frac{1}{\sqrt{5}}\end{pmatrix}$。

由于$P^{-1}AP=\begin{pmatrix}\lambda_1 & 0 \\ 0 & \lambda_2\end{pmatrix}$，故$A^n=P\begin{pmatrix}\lambda_1^n & 0 \\ 0 & \lambda_2^n\end{pmatrix}P^{-1}$，于是：

$$ \begin{aligned} \begin{pmatrix} F_{n+1} \\ F_n \end{pmatrix} & = A^{n} \begin{pmatrix}1 \\0\end{pmatrix}\\ & = \begin{pmatrix}1 & 1\\ \lambda_2 & \lambda_1\end{pmatrix} \begin{pmatrix}(\lambda_1)^n & 0 \\ 0 & (\lambda_2)^n\end{pmatrix} \begin{pmatrix} \frac{\sqrt{5}-1}{2\sqrt{5}}\\ \frac{1+\sqrt{5}}{2\sqrt{5}}\end{pmatrix}\\ & = \begin{pmatrix}1 & 1\\ \lambda_2 & \lambda_1\end{pmatrix} \begin{pmatrix}\frac{\sqrt{5}-1}{2\sqrt{5}}(\lambda_1)^n \\ \frac{1+\sqrt{5}}{2\sqrt{5}}(\lambda_2)^n\end{pmatrix} \end{aligned} $$

因此：

$$ \begin{aligned} F_n & = \lambda_2\cdot \frac{\sqrt{5}-1}{2\sqrt{5}}(\lambda_1)^n+\lambda_1\cdot\frac{1+\sqrt{5}}{2\sqrt{5}}(\lambda_2)^n\\ & = \frac{1}{\sqrt{5}}[(\lambda_2)^n-(\lambda_1)^n] \end{aligned} $$

参考：斐波那契数列通项公式是怎样推导出来的？ - 面无表情的仔仔的回答 - 知乎

利用通项公式计算#

这种方式本质上还是利用快速幂计算，不过不需要矩阵了。

首先考虑一下通项公式中的根号与分式如何处理，假设模数为$M$，以$\frac{1+\sqrt{5}}{2}$为例，假设$x\equiv\frac{1+\sqrt{5}}{2}\pmod{M}$，则有$(2x-1)^2\equiv5\pmod{M}$。

以$M=10^9+9$为例，直接暴力求出x。（需要运行几分钟，其实有更快的算法，但是较为复杂，就先不讲了）

M = 10**9 + 9
for x in range(1, M):
    if (2*x-1)**2 % M == 5:
        print(x)
# 运行结果：
# 308495997
# 691504013

另一个解是$\frac{1-\sqrt{5}}{2}$。同理计算出$\frac{1}{\sqrt{5}}$的结果为276601605、723398404，通过尝试我们可以找出正确的组合。

对应题目：51Nod1242 斐波那契数列的第N项

这样我们就可以写出非常简短的代码：

n, m, p, s = int(input()), 10**9+9, 308495997, 723398404
print(s*(pow(p,n,m)-pow(m-p+1,n,m))%m)

注：python的pow自带快速幂，时间复杂度仍然是$O(\log n)$。python实现的取模运算保证结果为非负数，因此减法部分不用考虑负数问题。

斐波那契数列相关难题#

部分题目来自：斐波那契数列的那些题。

这些题目十分有难度，后续会慢慢补上。。。

k次幂求和#

对应题目：51Nod1236 序列求和 V3、ZOJ3774 Power of Fibonacci

不妨设$\phi=\frac{1+\sqrt{5}}{2}$,$\bar\phi=\frac{1-\sqrt{5}}{2}$。

则有$F_n=\frac{1}{\sqrt{5}}(\phi^n-\bar\phi^n)$。

那么：$F_n^k=(\frac{1}{\sqrt{5}})^k(\phi^n-\bar\phi^n)^k$。

利用二项式定理展开得：

$$ F_n^k=(\frac{1}{\sqrt{5}})^k\sum_{i=0}^kC_k^i(\phi^n)^{k-i}(-\bar\phi^n)^i $$

求前缀和计算得：

$$ \begin{aligned} S_n & = \sum_{i=1}^nF_i^k\\ & = \sum_{i=1}^n(\frac{1}{\sqrt{5}})^k\sum_{j=0}^kC_k^j(\phi^i)^{k-j}(-\bar\phi^i)^j\\ & = (\frac{1}{\sqrt{5}})^k\sum_{i=1}^n\sum_{j=0}^k (-1)^j C_k^j \phi^{i(k-j)} \bar\phi^{ij}\\ \end{aligned} $$

变换求值顺序（将j看成定值）有：

$$ S_n = (\frac{1}{\sqrt{5}})^k\sum_{j=0}^k (-1)^j C_k^j \sum_{i=1}^n (\phi^{k-j} \bar\phi^j)^i\\ $$

不妨设$q=\phi^{k-j} \bar\phi^j$，若$q=1$，则$\sum\limits_{i=1}^n (\phi^{k-j} \bar\phi^j)^i=n$，否则利用等比数列求和公式计算得$\frac{q\cdot (1-q^n)}{1-q}$。
于是我们预处理出阶乘、以及两个常量的幂次，即可计算，时间复杂度$O(K+TK\log n)$。

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e5 + 5;
const ll M = 1e9 + 9;
ll phi[N], phj[N], fac[N];
#define FOR(i, a, b) for (int i = a; i < b; i++)
#define PRE(arr, n) arr[0] = 1; FOR(i, 1, N) arr[i] = arr[i-1]*n%M
ll qpow(ll x, ll y) {
    ll ans = 1;
    for (; y; y >>= 1) {
        if (y & 1) ans = ans * x % M;
        x = x * x % M;
    }
    return ans;
}
inline ll inv(ll x) { return qpow(x, M-2); }
int main() {
    ios::sync_with_stdio(false), cin.tie(0);
    PRE(fac, i); PRE(phi, 691504013); PRE(phj, 308495997);
    int t; cin >> t;
    while (t--) {
        ll n, k; cin >> n >> k;
        ll ans = 0;
        FOR(j, 0, k+1) {
            ll q = phi[k-j]*phj[j]%M;
            ll com = fac[k]*inv(fac[j]*fac[k-j]%M)%M;
            ll prod = (q==1) ? (n%M) : (q*(qpow(q,n)-1)%M*inv(q-1)%M);
            ans = (j&1) ? (ans-com*prod)%M : (ans+com*prod)%M;
        }
        cout << (ans*qpow(276601605, k)%M+M)%M << '\n';
    }
    return 0;
}

顺带一提，我还尝试用Python写这题（理论复杂度应该没有问题），发现可以通过51Nod（时限为18s）但是无法通过ZOJ（时限为5s）。从51Nod的测试结果来看，上面的C++程序只跑了不到1s，而Python写法最多要跑10s。

不同语言的时间限制和内存限制是相同的吗？
是相同的，我们认为选择合适的编程语言也是一项必备技能，所以没有为不同语言设置不同的限制条件。（来自ZOJ）

如果有知道如何优化Python时间的希望能留言告诉我一下。

点击展开代码 >folded

t, m, fac = int(input()), 10**9+9, [1]
for i in range(1, 100001): fac.append(fac[-1]*i%m) # 预处理阶乘
inv = lambda x: pow(x, m-2, m) # 计算逆元
phi, phibar = [1], [1]
for i in range(1, 100001): phi.append(phi[-1]*691504013%m)
for i in range(1, 100001): phibar.append(phibar[-1]*308495997%m)
for i in range(t):
    n, k = list(map(int, input().split()))
    ans = 0
    for j in range(k+1):
        q = phi[k-j]*phibar[j]%m
        com = fac[k]*inv(fac[j]*fac[k-j]%m)%m
        prod = n if q==1 else q*(m+1-pow(q, n, m))%m*inv(m+1-q)%m
        sgn = 1 if j%2==0 else -1
        ans = (ans + com*sgn*prod + m) % m
    print(ans*pow(276601605,k,m)%m)

大范围求循环节#

对应题目：51Nod1195 斐波那契数列的循环节

这题是之前小范围求循环节的加强版，质数的范围最大可以到$10^9$。可以再仔细阅读一下这篇论文：The Period of the Fibonacci Sequence Modulo j.pdf。

主要利用这条性质加速计算：

对于质数$p > 5$，如果5是模p的二次剩余，那么模p意义下的循环节长度是(p-1)的因子，否则是(2p+2)的因子。

利用欧拉判定准则来判断二次剩余。

代码中还用到了一些数论方面的知识，例如素数筛法、质因数分解、枚举因子、判二次剩余。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
// 质数表大小以及小范围常量表
const int N = 1e5, pd[6]{0, 1, 3, 8, 6, 20}; 
ll lcm(ll a, ll b) { return a / __gcd(a, b) * b; }
// 矩阵快速幂求斐波那契数列
ll fib(ll n, ll mod, ll a = 1, ll b = 0, ll p = 0, ll q = 1) {
    if (!n) return b;
    if (n & 1) return fib(n-1, mod, (b*q+a*q+a*p)%mod, (b*p+a*q)%mod, p, q);
    return fib(n/2, mod, a, b, (p*p+q*q)%mod, (q*q+2*q*p)%mod);
}
// 检查mod下循环节是否为perd
bool check_perd(ll mod, ll perd) {
    return fib(perd, mod)==0 && fib(perd+1, mod)==1;
}
vector<bool> is_prime;
vector<ll> prime;
// 素数筛法
void get_prime() { 
    is_prime.resize(N, true);
    is_prime[0] = is_prime[1] = false;
    for (ll i = 2; i < N; i++) {
        if (!is_prime[i]) continue;
        prime.push_back(i);
        for (ll j = i * i; j < N; j += i) is_prime[j] = false;
    }
}
// 质因数分解
vector<pair<ll, ll>> get_factor(ll n) {
    vector<pair<ll, ll>> factor;
    for (auto p : prime) {
        if (p > n / p) break;
        if (n % p) continue;
        int cnt = 0;
        while (n % p == 0) cnt++, n /= p;
        factor.emplace_back(p, cnt);
    }
    if (n > 1) factor.emplace_back(n, 1);
    return factor;
}
// 快速幂
ll pow(ll x, ll y, ll mod = 9e18, ll ans = 1) { 
    if (!y) return ans;
    if (y&1) return pow(x, y-1, mod, ans*x%mod);
    else return pow(x*x%mod, y>>1, mod, ans);
}
// 判断n是否为p的二次剩余
bool is_quad(ll n, ll p) { 
    return pow(n, (p-1)>>1, p) == 1;
}
// 枚举因子
vector<ll> perm_factor(ll n) {
    auto factor = get_factor(n);
    vector<ll> divisor;
    function<void(ll, int)> dfs = [&](ll d, int i) {
        if (i == (int)factor.size()) return divisor.push_back(d);
        for (ll j = 0; j <= factor[i].second; j++)
            dfs(d * pow(factor[i].first, j), i+1);
    };
    return dfs(1, 0), divisor;
}
// 求循环节
ll fib_pred(ll n) {
    if (n <= 5) return pd[n]; // 小于等于5的数不满足该性质
    ll t = is_quad(5, n) ? (n-1) : (2*n+2);
    for (auto d : perm_factor(t)) // 枚举所有t的因子
        if (check_perd(n, d)) return d;
    return assert(false), 0;
}
// 处理每一组数据
void solve() {
    ll n, ans = 1; cin >> n;
    for (auto f : get_factor(n))
        ans = lcm(ans, pow(f.first, f.second-1) * fib_pred(f.first));
    cout << ans << '\n';
}
int main() {
    ios::sync_with_stdio(false), cin.tie(0);
    get_prime();
    int t = 1; cin >> t;
    while (t--) solve();
    return 0;
}

参考博客

最小公倍数#

对应题目：51Nod1355 斐波那契的最小公倍数

找位置#

对应题目：51Nod1145 斐波那契数列

求$f(n)\mod f(k)$#

对应题目：51Nod1194 Fib(N) mod Fib(K)

广义斐波那契数列求循环节#

对应题目：1263 广义斐波那契数列

参考论文：PeriodRankOrderMMofficial.pdf

斐波那契字符串#

对应题目：51Nod 1146 斐波那契字符串

$\pi$斐波那契数列#

对应题目：51Nod1149 Pi的递推式